Timed Multiplication Tests: An Alternative

Timed Tests: An Alternative

Recently I was having a conversation with an elementary teacher who conveyed that her students were doing pretty well on their multiplication tables up to 12. I asked her if she felt they truly understood the meaning of multiplication. She indicated to me she thought so because most were doing quite well on their timed multiplication tests. There were a few stragglers but she felt most had it down even though she had to give a few students extra time to complete what she asked them to do. I asked her if she would be willing to engage in a thought experiment with me. She indicated that she would so asked her to walk into class the next day and put the problem 13 * 8 on the board and have her students reason about the problem. As I greeted her the next day she almost had tears in her eyes as she said, “They don’t really understand multiplication do they? All that time I spent on learning multiplication tables I thought my students were developing a deep understanding of multiplication! Not one of my students was able to make sense of this problem without some prompting from me. I even asked them what 12 * 8 and they told me it was 96 but not one of my students could reason from that to make sense of 13 * 8!”

I felt for her because I find myself in situations like this the more reflective I become. Thinking what I am doing is best for students’ understanding but having to make changes when the student understanding I desire is not really happening or there are pedagogical steps that do not quite fit together. I have been a classroom teacher for nearly 25 years and came to the realization two weeks that maybe all those years of talking about the slope of a line such as y = 3x + 2 as “right 1, and up 3”  "or rise 3 and run 1" was not mathematically sound. In order to accurately represent the multiplication of 3 in the equation I should have been saying, “for every horizontal change of 1, or any amount for that matter, the vertical change is 3 times that amount”--A statement that exemplifies the multiplicative reasoning that is reflected in the equation y = 3x + 2.

Although I was quite good at timed multiplication tests I have a disdain for them and quite honestly I would like to see them removed from every classroom in the United States! That being said I think it is important that an alternative is provided. Before getting started it is important to make one thing very clear---Every student should develop automaticity with his/her multiplication facts! None of us want a 6^th grade student having to pick up a calculator to compute 6 * 9. The desire is for something more than just automaticity. The desire is for them to have the fluency and reasoning capacity to make sense of a variety of situations and ideas involving multiplication and see how these ideas fits with other aspects of mathematics. Here is how I envision developing a deep understanding of multiplication, the representations needed to develop this understanding, and a sampling of the types of problems we can think about with a deep understanding of multiplication.

Let’s start by looking at the work my daughter, who is in 1^st grade, did to solve a multiplication problem she was presented [https://cloud.swivl.com/library/404951/share/public]. The problem was, “You have 8 friends and you want to give them 3 pieces of candy each. How many total pieces of candy will you need to do this?” I did not share with her that this was a multiplication problem. I simply gave her the task and watched as she made sense of the task. As you can see she started forming equal groups of 3 and created a tower with the number cubes to keep track of the number of groups that she had. She started to skip count by 3 up to 9 and then counted on up to 24.

I am not claiming that she understands multiplication but I do claim that she is starting to make sense of some important features of multiplication. That is the formation of equal-sized groups and the counting of those equal sized groups. The abstract version of the problem Gwen worked (i.e. 8 * 3) can be thought of as 8 equal-sized groups of 3 in which the 8 is the multiplier and the 3 is the multiplicative unit (which consists of 3 iterated units of 1)—You can see all these aspects in Gwen’s work.

Another important idea embedded in Gwen’s work is repeated addition. The abstract problem 8 * 3 can be thought of as 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3. While starting to skip count which would model this abstract notion Gwen technically modeled 3 + 3 + 3 + 1 + 1 + 1 …. + 1 until she reached 24.

Before going too much further I think it is important for me to share one of my biases. I believe the development of multiplication concepts should involve visual models. Here is why I believe this is important. There is a difference between “number” and “numeral”—I believe this is a big idea that we gloss over simply because we are adults and live the in the “numeral” world.  Reflect for a moment on the numeral “3”. What meanings do you have associated with it?  This is a symbol whose meaning is entirely based on an understanding of “threeness”. I guarantee that your understanding of ‘3’ is attached to some visual representation of a number of objects. One of my colleagues, Dr. Cheryl Lubinksi, has drilled this phrase into my head, “See number, write numeral!” We have to visualize the meaning of number (concrete) before we can make sense of the meaning of the numeral (abstract). I believe the same is true when we start performing operations with those numbers.

Let’s spend a few moments talking about the abstract version (i.e. 8 * 3) of the problem presented to Gwen by making the problem visually concrete using an array of counters.

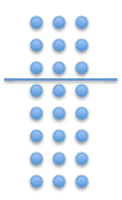
Unlike modeling addition (e.g. 8 + 3) in which each of the numerals can be represented by the number of counters represented by each numeral modeling multiplication requires a coordination that involves seeing equal sized sets of numbers. Seeing the array of counters as representing multiplication requires coordinating the number of equal sized groups {8} with the size of each of those groups {3} to determine the total number of counters in the array {24}. 

As stated earlier one of my goals is to develop fluency with numbers along with rich, powerful connections that can be exemplified within these representations. Commutativity and Distributivity are powerful properties of multiplication. Unfortunately, many times these powerful ideas are first presented abstractly in algebra devoid of any connection to relationships involving numbers. An array model of multiplication enables students to make sense of both of these ideas visually and in a way that may help them develop fluency with numbers. For example, rotating the array model of 8 groups of 3 ninety-degrees illuminates commutativity.  That is, it is easy for a child to make sense of the fact that 8 groups of 3 has the same number of counters as 3 groups of 8.

In a similar manner using an array of counters distributivity of multiplication over addition can be made sense of and used to reason about operations involving numbers. Suppose a child is not ready to handle 8 groups of 3 but the 8 groups of 3 can be partitioned into 5 groups of 3 {15} and into 3 groups of 3 {9}.

As a means to build fluency with numbers distributivity of multiplication can be used to mentally compute problems such as the one presented at the beginning of the discussion (i.e. 13 * 8). Using distributivity of multiplication over addition 13 groups of 8 can be re-grouped as 10 groups of 8 {80} and 3 groups of 8 {24} yielding an answer of 104. This idea becomes significantly more important as students seek to understand the structure of two-digit by two-digit multiplication.

There is another important idea that can facilitate number fluency with respect to multiplication. That is the idea of “halving and doubling”. For example, consider the multiplication problem 12 * 45. Halving the 12 {6} and doubling the 45 {90} the multiplication problem 6 * 90 can be more easily handled mentally and has the same answer as 12 * 45. The question is why? Consider the original problem 8 * 3 represented in an array model. If number of groups is halved and size of the groups is doubled one case see that an array 4 by 6 has the same number of counters as an array 8 by 3 {24}.

“Halving and doubling” is an idea that be extended to “thirding and tripling” and “fourthing and quadrupling” to give students powerful strategies to reason about multiplication. The power is in understanding why the strategy works and how the idea is connected to other ideas in mathematics. Halving and doubling numbers in a multiplication problem involves applying the relationship between a number and its reciprocal. A number, not zero, multiplied by its reciprocal will always equal 1. Abstractly when we “half and double” 8 * 3 to get 4 * 6 what we are doing is the computation 8* (1/2) * 3 * (2) which yields 4 * 6. It is also easy to see using the associative property of and commutative property of multiplication the relationship between multiplying by 2 and multiplying by its reciprocal 1/2 (i.e. (8 * 3) * (2 * (1/2)) = (8 * 3) * (1)).

Understanding the structure of multiplication in terms of visual representations provides students the mathematical power to reason about other multiplication problems. For example, starting with an understanding of the structure of 8 * 3 a student should be able to make sense and reason about the following multiplication problems 8 * 30, 4 * 6, 16 * 1.5, 18 * 3, 8 * 13, 16 * 3, .8 * 3, as well as many others.